Circles captivate us, and inscribed circles doubly so. In a previous post, we tackled finding the area of a shaded region. Today we pursue a similar goal with a twist.

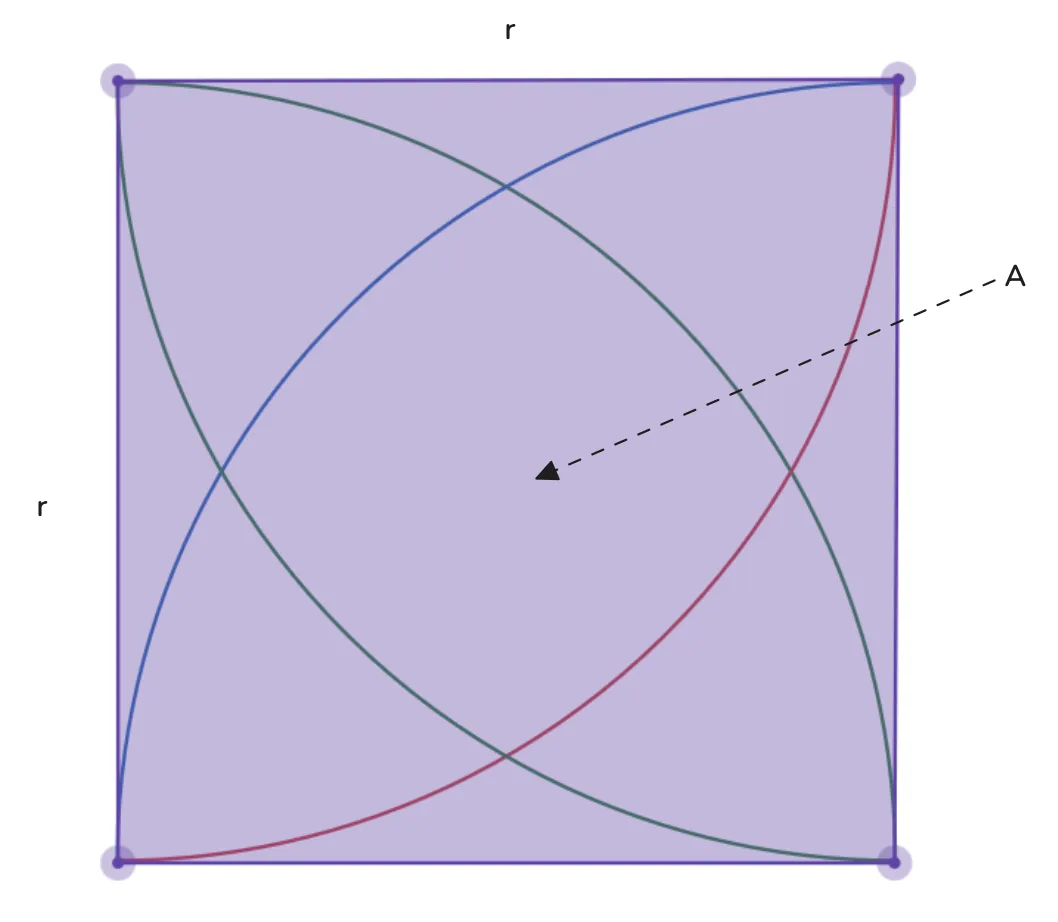
Here we have an r×rr \times r square containing four inscribed circles, each also of radius rr. Our mission: find the total area of that diamond-shaped region nestled in the center.

While numerical integration could solve this, we’ll take the geometric route. Our focus here is building intuition and strategy, not wrestling with integrals.

Oh Geometry!

When tackling geometric puzzles, I like to inventory what we already know and build from there.

Our toolkit includes familiar formulas: squares have area r2r^2, circles have area πr2\pi r^2, and triangles with base bb and height hh have area 12bh\frac{1}{2}bh. From our previous exploration, we also have a formula for the area of a chord segment that depends on the subtended angle θ\theta and radius rr—let’s call this Achord(r,θ)A_{\text{chord}}(r, \theta).

Time to R3R3 this problem1. Consider the following decomposition:

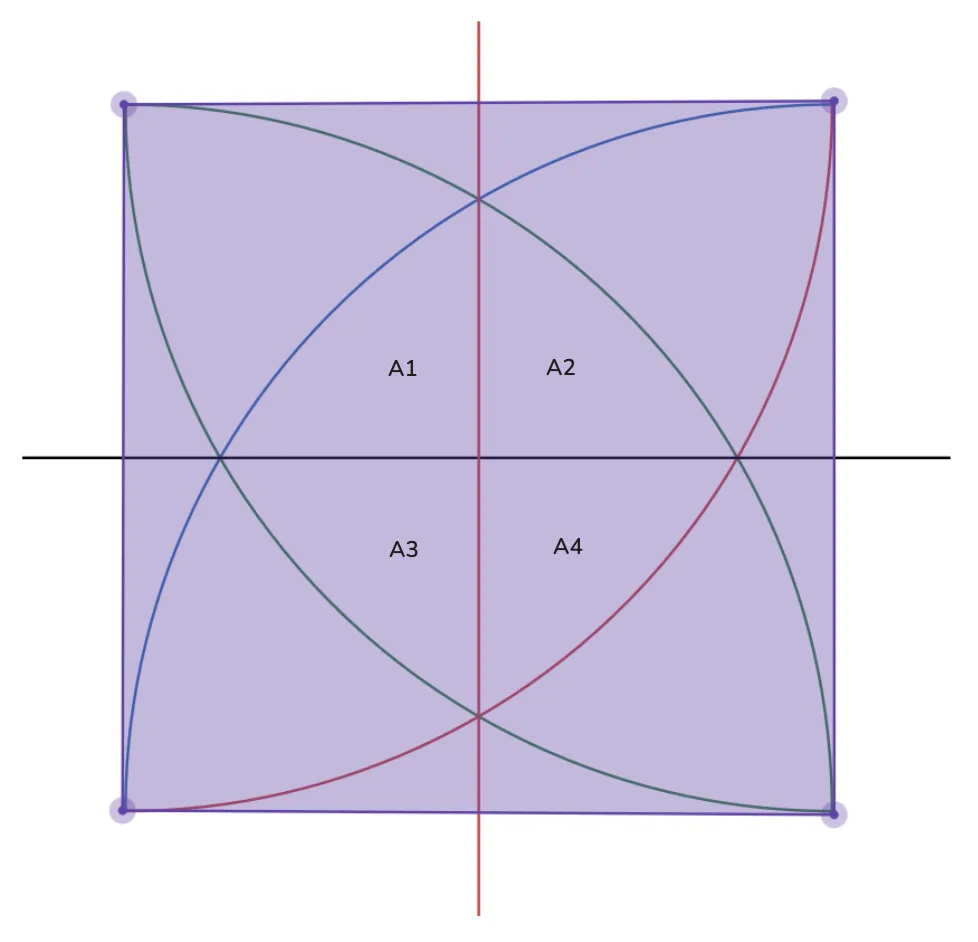
We’ve divided our diamond into four equal2 curved triangles, each bounded by its corresponding circle.

Area=A1+A2+A3+A4\text{Area} = A_1 + A_2 + A_3 + A_4

Since these areas are equal, we need only compute A1A_1 and multiply by four. Let’s zoom in on A1A_1—the diagram below looks complex at first, but will clarify our approach.

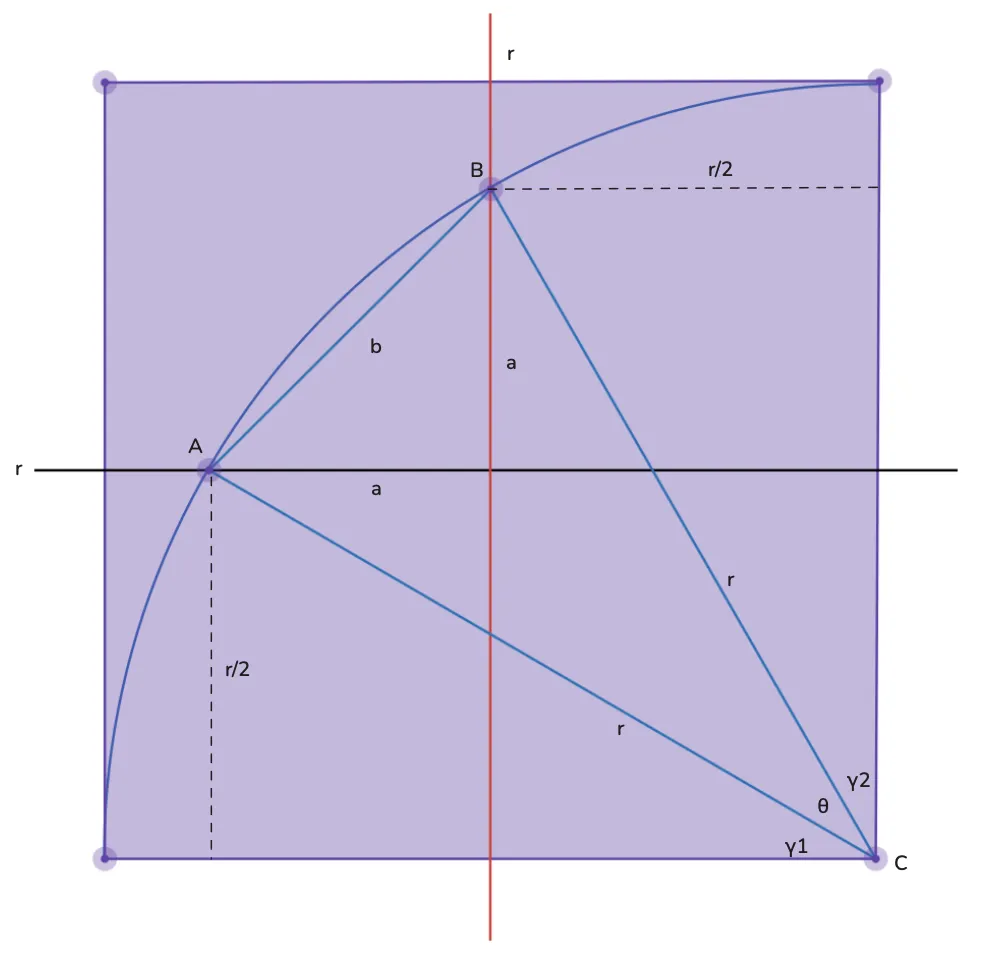
I’ve isolated the curve corresponding to A1A_1 and added sector ABCABC for reasons that will soon become apparent. Our target region sits in the upper-left quadrant.

From the diagram, A1A_1 equals the area of chord segment ABAB plus the triangular area a22\frac{a^2}{2}.

For the area of chord segment ABAB, we recall from our previous post:

Achord(r,θ)=12r2(θ−sin⁡θ)A_{\text{chord}}(r, \theta) = \frac{1}{2}r^2 \left( \theta - \sin\theta \right)

where θ\theta (in radians) is the angle subtended by chord ABAB at the circle’s center.

Therefore:

A1=a22+Achord(r,θ)A1=a22+12r2(θ−sin⁡θ)\begin{align} A_1 = \frac{a^2}{2} + A_{\text{chord}}(r, \theta) \\ A_1 = \frac{a^2}{2} + \frac{1}{2}r^2 \left( \theta - \sin\theta \right) \end{align}

Now we face a choice: equation (2)(2) involves both aa and θ\theta. To get a single-variable function A1(⋅)A_1(\cdot), which should we eliminate?

From the diagram, θ\theta appears more tractable. It’s constrained by θ+γ1+γ2=π2\theta + \gamma_1 + \gamma_2 = \frac{\pi}{2}; the angles at the square’s corner sum to a right angle.

So we’ll express aa in terms of θ\theta. Fortunately, the geometry cooperates: aa relates to bb via Pythagoras, and bb connects to θ\theta and rr through sector ABCABC.

a=b2b=2rsin⁡(θ2)\begin{align} a &= \frac{b}{\sqrt{2}} \\ b &= 2r\sin\left(\frac{\theta}{2}\right) \end{align}

Equation (4)(4) follows from sin⁡(θ2)=b2r\sin\left(\frac{\theta}{2}\right) = \frac{b}{2r}.

Substituting into equation (2)(2):

A1(θ)=a22+12r2(θ−sin⁡θ)=(b2)22+12r2(θ−sin⁡θ)=b24+12r2(θ−sin⁡θ)=r2sin⁡2(θ2)+12r2(θ−sin⁡θ)\begin{align} A_1(\theta) &= \frac{a^2}{2} + \frac{1}{2}r^2 \left( \theta - \sin\theta \right) \\ &= \frac{\left(\frac{b}{\sqrt{2}}\right)^2}{2} + \frac{1}{2}r^2 \left( \theta - \sin\theta \right) \\ &= \frac{b^2}{4} + \frac{1}{2}r^2 \left( \theta - \sin\theta \right) \\ &= r^2\sin^2\left(\frac{\theta}{2}\right) + \frac{1}{2}r^2 \left( \theta - \sin\theta \right) \\ \end{align}

Excellent! Now A1A_1 depends only on θ\theta.

The Final Stretch

Nearly there! The diagram suggests θ\theta has a fixed value. Returning to the square’s bottom-right corner, we have θ+γ1+γ2=π2\theta + \gamma_1 + \gamma_2 = \frac{\pi}{2}.

Both γ1\gamma_1 and γ2\gamma_2 are determined by right triangles with hypotenuse rr and shorter leg r2\frac{r}{2}. Basic trigonometry gives:

γ1=arcsin⁡(r/2r)=arcsin⁡(12)=π6\gamma_1 = \arcsin\left(\frac{r/2}{r}\right) = \arcsin\left(\frac{1}{2}\right) = \frac{\pi}{6}

By symmetry:

γ2=arcsin⁡(12)=π6\gamma_2 = \arcsin\left(\frac{1}{2}\right) = \frac{\pi}{6}

Now we can find θ\theta:

θ=π2−γ1−γ2=π2−π3=π6\begin{align} \theta &= \frac{\pi}{2} - \gamma_1 - \gamma_2 \\ &= \frac{\pi}{2} - \frac{\pi}{3} \\ &= \frac{\pi}{6} \end{align}

Substituting θ=π6\theta = \frac{\pi}{6} into equation (8)(8):

A1=r2sin⁡2(θ2)+12r2(θ−sin⁡θ)=r2sin⁡2(π12)+12r2(π6−sin⁡π6)=r2(sin⁡2(π12)+π12−12sin⁡π6)\begin{align} A_1 &= r^2\sin^2\left(\frac{\theta}{2}\right) + \frac{1}{2}r^2 \left( \theta - \sin\theta \right) \\ &= r^2\sin^2\left(\frac{\pi}{12}\right) + \frac{1}{2}r^2 \left( \frac{\pi}{6} - \sin\frac{\pi}{6} \right) \\ &= r^2\left(\sin^2\left(\frac{\pi}{12}\right) + \frac{\pi}{12} - \frac{1}{2}\sin\frac{\pi}{6}\right) \\ \end{align}

The diamond’s total area is simply four times A1A_1:

Area=4A1=4r2(sin⁡2π12+π12−12sin⁡π6)□\text{Area} = 4A_1 = 4r^2\left(\sin^2\frac{\pi}{12} + \frac{\pi}{12} - \frac{1}{2}\sin\frac{\pi}{6}\right) \square

Mission Accomplished

We’ve found our diamond’s area! The result depends only on rr and scales quadratically—exactly what we’d expect. As a sanity check, try plotting this for r=1r=1 in Desmos and count grid squares3.

A delightful discovery: our angle θ\theta always equals π6\frac{\pi}{6}, independent of rr. This geometric invariant elegantly confirms that our area formula depends solely on the radius.

Thanks for reading!

Footnotes

  1. If you’ve forgotten, this stands for reject, reframe, and reduce and should be read in the same spirit as “gaslight, gatekeep, girlboss”. ↩

  2. Symmetry guarantees equality—the diamond mirrors the square’s symmetry, and we’ve partitioned the square into four equal r2×r2\frac{r}{2} \times \frac{r}{2} regions. ↩

  3. Challenge: define one function f1(x)f_1(x) for a single curve, then construct the other three using transformations like f2(x)=f1(x)+rf_2(x) = f_1(x) + r. ↩